Wave Calculation : Morison Equation

1. Waves and offshore Structures

The primary hydrodynamic forces acting on offshore structures are generated by pressure and drag. The contribution of pressure and drag varies depending on wave conditions and the geometric shape of the offshore structure. The interaction between offshore structures and waves is significantly influenced by the relative sizes of the structure and the wavelength. For instance, if the offshore structure has a circular cross-section with a diameter of D and the wavelength is λ, when λ is small, wave deformations caused by the offshore structure, such as diffraction and reflection, can be disregarded. However, when λ is large, these wave deformations need to be considered.

The determination of the size of offshore structures is based on the relative size with respect to the wavelength. For example, when ocean waves pass through a pile, the wavelength of the ocean waves is about 50 to 100 times the diameter of the pile. Therefore, wave deformations at a distance equal to one wavelength from the pile appear as if unaffected by the pile. In this case, the pile can be considered a small offshore structure. By ignoring the interaction between waves and offshore structures, the calculation of the hydrodynamic forces acting on small offshore structures becomes simpler. In other words, in this case, the effect of waves on the pile is calculated, but it is assumed that the pile has no impact on the waves. Thus, the hydrodynamic forces are simply a function of incident waves at the location of the pile.

On the contrary, consider a platform floating on waves with small wavelengths. While some waves propagate around or beneath the platform, many incident waves are reflected by the platform. Therefore, it is essential to consider such wave deformations in the calculation of hydrodynamic forces for platforms floating on waves with small wavelengths.

2. The Morison Equation

For small subsea structures, the deformation caused by incident waves is not significant. If the diameter of a subsea structure is less than 5% of the wavelength, this assumption is considered valid. Representative small subsea structures meeting these conditions include piles, subsea components of platforms, pipelines, moorings, and more. The most commonly used method for estimating the hydrodynamic forces acting on these small subsea structures is the Morison equation. This equation has been widely utilized since the 1950s to calculate wave loads on offshore structures, especially for structures where the size of components is relatively small compared to the wavelength.

The Morison equation consists of inertia force and drag force, excluding hydrostatic force. In this context, inertia force is related to the pressure acting on the subsea structure, while drag force is associated with the friction and separation of water flow around the subsea structure.

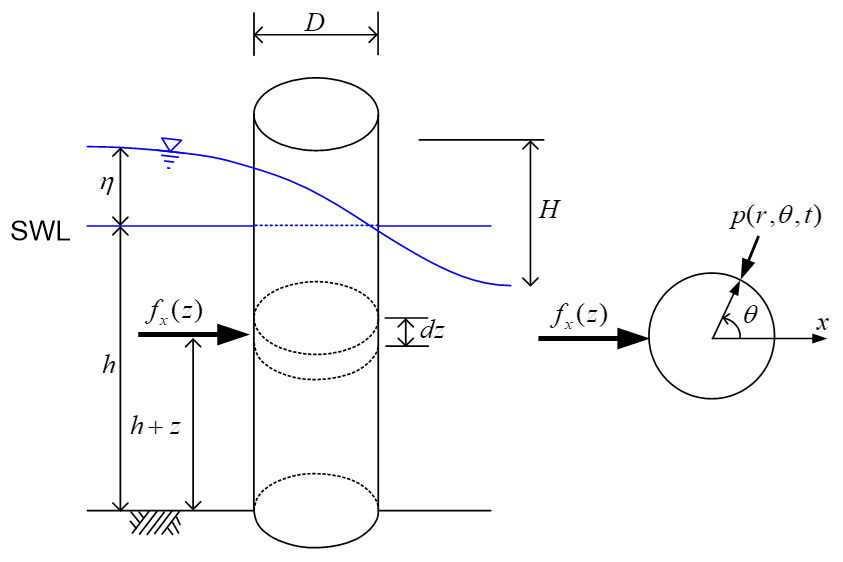Fig. 1 A circular cylinder placed vertically in water

If we derive the Morison equation to calculate the wave force acting on a vertical cylinder placed in water, the horizontal component of the wave force acting per unit length of the cylinder is as follows.

This load, which is related to fluid pressure, is proportional to the acceleration of the flow through a fixed cylinder and is therefore called ‘inertia force’. It can be seen that this load is twice as large as the general inertial force as shown below:

which is expressed as the product of mass (i.e., the mass of fluid excluded by the cylinder) and acceleration. Therefore, the inertial force due to flow is expressed as follows using general inertial force.

Here, Ca is the ‘added mass coefficient.’ In rigid body dynamics, the inertial force is simply related to the mass of the rigid body, but it can be seen that the mass of the fluid accelerated in the fluid is greater than the mass of the fluid simply displaced by the cylinder. For reference, the added fluid mass is called ‘added mass’. Previously, we showed that Ca= 1 for a vertical circular cylinder, and Ca can be obtained analytically for simple geometric cross sections and flows. In general, the ‘inertia coefficient (Cm = 1 + Ca)’ is newly defined, and the inertia force due to flow is expressed as follows.

Although the inertial force (f_ix) was obtained assuming an ideal fluid, drag also exists in real fluids, and drag can be divided into 1) ‘skin drag’ and 2) ‘form drag’. Both of these drag forces are proportional to the square of the speed and the empirical coefficients (which are functions of Reynolds number, geometry, roughness, etc.), and are represented by one drag force, which can be expressed in the formula as follows.

Here, f_dx is the drag force acting per unit length of the cylinder; Cd is the ‘drag force coefficient’; u is the founder speed in the direction of wave propagation.

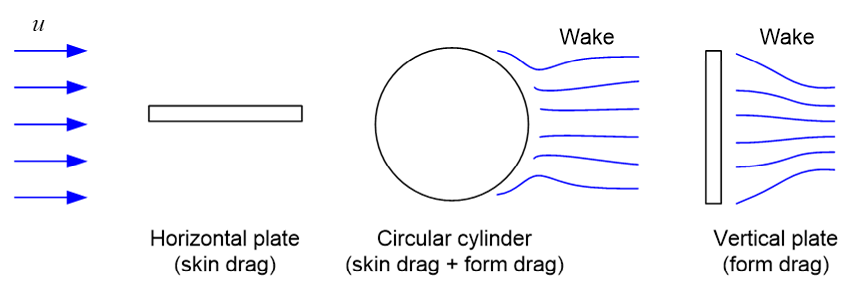Fig. 2 Drag Force

Ultimately, the wave force acting per unit length of the cylinder is the sum of drag force (f_dx) and inertial force (f_ix) and can be expressed as the following ‘Morison equation’.

Here, the velocity and acceleration of the erector are calculated assuming that the cylinder does not exist at the center point of the cylinder. If the cylinder moves, the following wave force is calculated using the drag and inertial force obtained using the relative velocity and relative acceleration between the fluid and the structure, and this equation is called the 'relative motion Morison equation. 'It is said.

Here, x represents the horizontal displacement of the structure.

In the Morison equation, the maximum values of drag force and inertia force do not occur simultaneously, and since Cd and Cm do not vary significantly, the relative importance of the drag force component and inertia force component is mainly influenced by the 'Keulegan-Carpenter number (Kc).

This number is a value that represents the distance the erector moves (u_mT) relative to the diameter of the pile (D). If Kc is large, the erector moves relatively much compared to the diameter of the cylinder, which is similar to the condition of ‘steady flow’. Here, steady flow refers to a uniform and smooth flow with a 'Raynolds number' of less than 1000. The speed of the fluid appears constant regardless of time (i.e., is uniform), and the streamlines are continuous and do not intersect each other ( i.e. smooth). In steady flow, there is no inertial force, so the total wave force consists only of the drag component. Conversely, if Kc is small, the erector moves relatively little compared to the diameter of the cylinder, and the inertial force component rather than the drag component dominates the total wave force.

3. Drag & Inertia Coefficient

Load coefficients (i.e. drag coefficient Cd and inertia coefficient Ci) are determined empirically through laboratory or field measurements. Experimental coefficients can be obtained for several flows such as steady flow, oscillatory flow, wave flow, etc., and correction is required to apply these coefficients to actual flows. For example, in the case of ‘oscillatory flow’, the waveform moves horizontally back and forth, but the actual wave moves in orbital motion. 

Additionally, an appropriate pylon must be selected to analyze data obtained through laboratory or field measurements. Linear wave theory can be applied to small underwater objects, but nonlinear wave theory can also be applied depending on actual needs.

You can check more of these details in the download file.

3. Drag & Inertia Coefficient

4. Linear Morison equation

References

Doogi Kim, Structural Dynamics, Gumi Library, 2005/2009.

Choi Hang-soon, Consideration on wave loads acting on marine structures, Journal of the Korean Society of Shipbuilding, 18(2), 49-55, June 1981.

Tedesco, J.W., McDougal, W.G., Ross, C.A. (1999). Structural Dynamics: Theory and Applications, Addison-Wesley, Menlo Park, CA.

SynClaire, http://synclaire.net.

Wikipedia encyclopedia site, http://en.wikipedia.org.

Topics

#Hydrodynamic forces
#Morison equation
#Offshore structures

About the Editor

Harold S.Y Ha

Structural Engineer(Motivator) More than 15 years of experience

I am a structural engineer who is interested in all structures from civil structures to offshore structures.
Based on various practical experiences, I would like to introduce engineering more easily.
And I want to be able to share my thoughts and enjoy the various attempts that can improve the efficiency of engineering work with you.

I hope every engineer who reads my contents will get even the slightest inspiration and motivation needed for the engineer's journey.

 

👉 Learn more about the editor (click)

※ Click on the keywords below 'Topics' to view related content.