Advancing FEA: High-Order Triangular Elements Explained

For the previous example, we can use high-order triangular elements. This element has six nodes per element and assumes the displacement is quadratic within an element. Also, each side edge can be curved, as shown.

Let’s start with two elements.

Geometry, Two high-order triangular element case

The FEA results in deflection = 0.285 in. and stress = 50.73 ksi. These are much better than those from linear triangular elements, but still way off. As shown, we can increase the number of divisions, say a total of 32 elements. 

Geometry, 32 high-order triangular element case

As can be expected, the results are much better and close to so-called exact values.

In the high-order triangular element, the displacement varies as quadratic (in other words, the shape function is quadratic) within an element. So the strain/stress varies linearly because strain/stress is one order lower than displacement, which is why this element is also called a linear (not constant) strain element.

The stress in this example varies linearly both in the horizontal and vertical axis. We know high-order triangular elements can consider this linear variation. Why we cannot get the exact results only with two elements?

With the given loading condition, the strain/stress varies linearly in the horizontal and vertical directions but not in the diagonal (connection line between two elements). However, in the high-order triangular element, linear variation is also assumed in this diagonal direction. If we consider the pure bending condition (M=10 ft-kips at the tip), we can get almost exact results only with two elements as shown. The minor differences are due to shear deformation.

Stress (ksi), Two high-order triangular element case, Pure bending case

The exact values from beam theory are

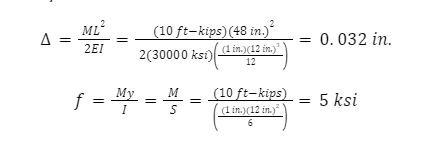Pure bending case

We can see that the accuracy from FEA depends on the number of divisions and the loading condition itself. For the same structure, sometimes we can get correct results only with two elements but wrong results even with 128 elements. This is one of the reasons why we need to understand the theory behind the FEA program.

2 HIGH ORDER TRIANGULAR METHODS [Click]

32 HIGH ORDER TRIANGULAR METHODS [Click]

About the Editor

Seungwoo Lee, Ph.D., P.E., S.E.

Senior Supervising Engineer WSP USAs (Tampa, FL)

He is a Senior Supervising Engineer with a high level of expertise in the design and analysis of suspension bridges. He has a solid fundamental understanding of structures and can apply his knowledge exceptionally well to the design and analysis of highly complex structures. He is also a strong communicator, able to identify and distill the key information that is relevant to the task at hand and present it in a clear and quickly understandable manner.