Creep Analysis 5 MIDAS Example
In this article, the previous method explained in Creep Analysis 4 is applied to a real-world bridge and compares the output with MIDAS??
Consider a two-span bridge as shown below.
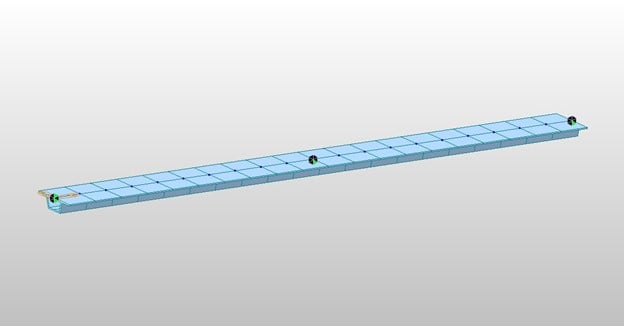Two-span bridge
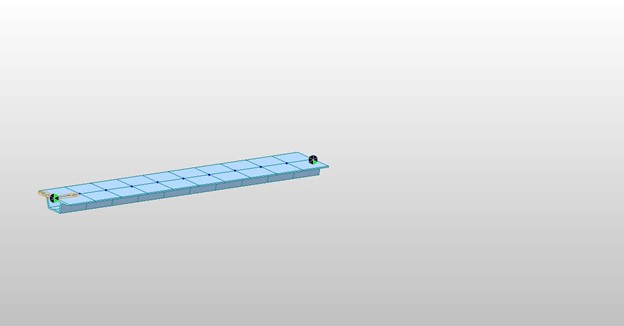Stage 1
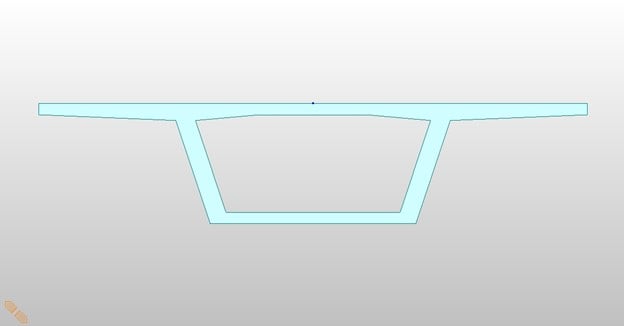Typical section
Section properties are:
|
Area |
46.5119 ft2 |
|
Moment of Inertia |
303.5361 ft4 |
|
Perimeter (outside) |
74.0359 ft |
|
Perimeter (inside) |
35.1884 ft |
Material properties are:
|
f'c |
6 ksi |
|
RH |
70% |
| Concrete |
Normal and rapid hardening |
Creep Coefficient
Elastic Modulus (MPa)
From the graph,
φ(∞, 7) = 2.19 χ(∞, 7) = 0.74 φ(60, 7) = 0.975
φ(∞, 60) = 1.46 χ(∞, 60) = 0.82.
Ec(60)/Ec(7) = 1.040/0.882 = 1.179.
At time t1 = 60 days, the member end forces due to self-weight at span 2 can be calculated as below. Note that Ec(60)/Ec(7) = 1.179. (MIDAS file ex.2C)
[Member End Force] = [Stiffness]{Displacement} + {Fixed End Force}
[Stiffness]{Displacement} = [Member End Force] - {Fixed End Force}
Analyze two-span continuous beam for these member end loadings. Note that the section properties are as below and the loading directions may not be identical for each program. (MIDAS file ex.2D)
Results (ft, kips)
Finally, the member end forces are:
Span AB
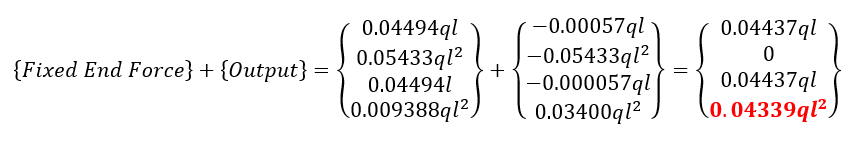
Span BC
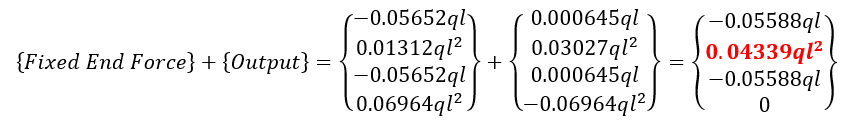
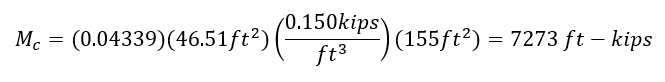
Check this result with MIDAS output (MIDAS file ex.2E).
Creep secondary moment (ft-kips)
Construction analysis from MIDAS gives creep secondary moment at pier 2 as 6866 ft-kips. The error between the two methods is 6% and again we do not know where these differences come from. However, considering the uncertainty of creep itself, the author believes this error is acceptable in practical design.
He is a Senior Supervising Engineer with a high level of expertise in the design and analysis of suspension bridges. He has a solid fundamental understanding of structures and can apply his knowledge exceptionally well to the design and analysis of highly complex structures. He is also a strong communicator, able to identify and distill the key information that is relevant to the task at hand and present it in a clear and quickly understandable manner.
